背包问题整理
背包定义
那么什么样的问题可以被称作为背包问题?换言之,我们拿到题目如何透过题目的不同包装形式看到里面背包问题的不变内核呢?
我对背包问题定义的理解:给定一个背包容量target,再给定一个数组nums(物品),能否按一定方式选取nums中的元素得到target。
注意:
- 背包容量target和物品nums的类型可能是数,也可能是字符串
- target可能题目已经给出(显式),也可能是需要我们从题目的信息中挖掘出来(非显式)(常见的非显式target比如sum/2等)
- 选取方式有常见的一下几种:每个元素选一次/每个元素选多次/选元素进行排列组合
背包问题的分类
常见的背包类型主要有以下几种:
- 01背包问题:每个元素最多选取一次
dp[i][j]表示从0-i个物品中选择不超过重量j的物品的最大价值 - 完全背包问题:每个元素可以重复选择
-
多重背包问题:每个元素是有限个的
- 组合背包问题:背包中的物品要考虑顺序
- 分组背包问题:不止一个背包,需要遍历每个背包
而每个背包问题要求的也是不同的,按照所求问题分类,又可以分为以下几种:
- 最值问题:要求最大值/最小值
- 存在问题:是否存在…………,满足…………
- 组合问题:求所有满足……的排列组合
因此把背包类型和问题类型结合起来就会出现以下细分的题目类型(几乎可以涵盖力扣上所有的背包问题):
- 背包最值问题
- 01背包存在问题
- 01背包组合问题
- 完全背包最值问题
- 完全背包存在问题
- 完全背包组合问题
- 分组背包最值问题
- 分组背包存在问题
- 分组背包组合问题
01背包
01背包:有n种物品与承重为m的背包。每种物品只有一件,每个物品都有对应的重量weight[i]与价值value[i],求解如何装包使得价值最大。
为什么叫它01背包呢,因为装进去就是1,不装进去就是0.所以针对每个物品就两种状态,装,不装。所以只要背包有足够大的空间,这个物品是有可能被装进去的咯。所以有状态转移方程:dp[i][j] = max( dp[i-1][j] , dp[i-1][ j - weight[i] ] + value[i] )
// 0-1背包问题母代码(二维)
public int bags(){
int[] weight = new int[]{1,3,4}; // 各个物品的重量
int[] value = new int[]{15,20,30}; // 各个物品对应的价值
int bagWeight = 4; // 背包最大容量
// 状态定义:dp[i][j]表示从0-i个物品中选择不超过重量j的物品的最大价值
int[][] dp = new int[weight.length()+1][bagWeight+1];
// 初始化:第一列都是0(背包重量为0时啥都翻不了,价值都为0);第一行表示只选0号物品时的最大价值(首先要保证能容纳下0号物品的重量)
for(int j = weight[0]; j <= bagWeight ; j++){
dp[0][j] = dp[0][j-weight[0]] + value[0];
}
// 遍历方向:当前状态只与正上方和左上方的那行相关
for(int i = 1; i< weight.length(); i++){ // 遍历物品(第0个物品已经初始化了)
for(int j = 0; j <= bagWeight; j++){ // 遍历背包容量
if(j < weight[i]){ // 背包容量已经不足以放下第i个物品,因此最大价值就和上一个状态一致
dp[i][j] = dp[i-1][j];
}else{
// 背包容量足够,可拿可不拿:拿了最大价值是前i-1个物品扣除第i个物品的 重量的最大价值加上i个物品的价值
// 不拿就是前i-1个物品的最大价值,两者进行比较取较大的
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);
}
}
}
return dp[weight.length()-1][bagWeight];
}
二维代码可以进行优化,去除选取物品的那一层,简化为一维背包。其实就是把状态压缩,都在同一行做处理。
public int bags(){
int[] weight = new int[]{1,3,4}; // 各个物品的重量
int[] value = new int[]{15,20,30}; // 各个物品对应的价值
int bagWeight = 4; // 背包最大容量
// 状态定义: dp[j]表示容量为j的背包能放下东西的最大价值。
// 初始化: dp[0]=0
int[] dp = new int[bagWeight+1];
// dp[i][j] 都是通过上一行 dp[i-1][..] 转移过来的,之前的数据都不会再使用了。
for(int i = 1; i< weight.length(); i++){ // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--){ // 逆向遍历是为了防止覆盖状态,j<=weight[i]时,dp[j]=dp[j]可以省略;也可以理解成防止重复添加数据
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); // 不取或者取第i个
}
}
return dp[bagWeight];
}
完全背包
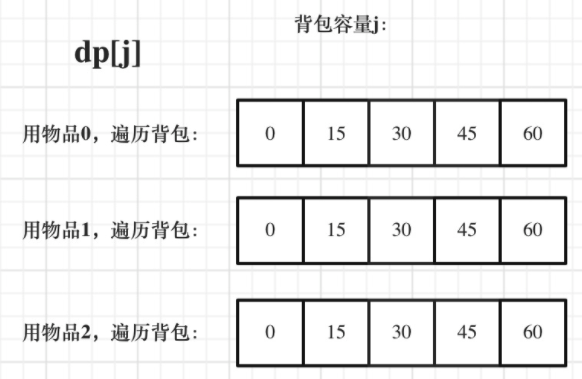
完全背包:有n种物品与承重为m的背包。每种物品有无限多件,每个物品都有对应的重量weight[i]与价值value[i],求解如何装包使得价值最大。
在下面的讲解中,我依然举这个例子:背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
首先在回顾一下01背包的核心代码:
for(int i = 1; i< weight.length(); i++){ // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--){ // 逆向遍历是为了防止覆盖状态,j<=weight[i]时,dp[j]=dp[j]可以省略;也可以理解成防止重复添加数据
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); // 不取或者取第i个
}
}
我们知道01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
// 先遍历物品,再遍历背包
// dp[i][j]表示从0-i个物品中选择不超过重量j的物品的最大价值
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
dp状态图:
背包问题解题模板
背包问题大体的解题模板是两层循环,分别遍历物品重量weight和背包容量bagWeight,然后写转移方程,根据背包的分类我们确定物品和容量遍历的先后顺序,根据问题的分类我们确定状态转移方程的写法。
首先是背包分类的模板(先要明确题目中的weight数组和bagWeight到底是什么):
- 01背包:
外循环物品重量, 内循环背包容量, bagWeight 倒序且 >= weight[i] - 完全背包:
外循环物品重量, 内循环背包容量, bagWeight 正序且 >= weight[i] - 组合背包(考虑顺序):
外循环背包容量, 内循环物品重量, bagWeight 正序且 >= weight[i] - 分组背包:这个比较特殊,需要三重循环:外循环背包bags,内部两层循环根据题目的要求转化为1,2,3三种背包类型的模板
然后是问题分类的模板:
- 最值问题(最大价值,最少硬币数之类的):
dp[j] = max/min(dp[j], dp[j - weight[i]] + 1)或dp[j] = max/min(dp[j], dp[j - weight[i]] + vlaue[i]) - 存在问题(bool):
dp[j] = dp[j] || dp[j - weight[i]] - 组合问题(装满背包有几种方法):
dp[j] += dp[j - weight[i]]
LeetCode!
| 题目 | 算法思想 |
|---|---|
| #322. 零钱兑换 | 完全背包最值问题:外循环coins,内循环amount正序 |
| #494. 目标和 | 0-1背包不考虑元素顺序的组合问题:选nums里的数得到target的种数,外循环nums,内循环target倒序 |
| #416. 分割等和子集 | 0-1背包存在性问题:是否存在一个子集,其和为target=sum/2,外循环nums,内循环target倒序 |
| #518. 零钱兑换 II | 完全背包不考虑顺序的组合问题:外循环coins,内循环target正序 |
| 279. 完全平方数 | 完全背包的最值问题:外循环nums,内循环target正序 |
| 377. 组合总和 Ⅳ | 考虑顺序的组合问题:外循环target,内循环nums |
| 1049. 最后一块石头的重量 II | 0/1背包最值问题:外循环stones,内循环target=sum/2倒序 |
既已览卷至此,何不品评一二: